Concentration and Activity
Plugging the Right Numbers Into Energy Calculations
(Thanks to Robert Lindquist, whose book* straightened me out on some of these matters.)
This page is originally authored by Gale Rhodes (© Jan 2000) and is still under continuous update.
The page has been modified with permission by Claude Aflalo (© Jan 2000).
Consider the reaction
2 NADH + 2H+ + O2 --> 2 NAD+ + 2 H2O
occurring in aqueous solution at pH 7.6, [NAD+] = 20.0 mM,
[NADH] = 10.0 mM, and oxygen at a partial pressure of 100.0 torr.
The free-energy change for this oxidation of NADH by oxygen is

What numbers should you plug in for the concentration terms?
These terms are properly activities, not concentrations. To convert
each concentration into activity, divide it by its standard concentration.
This eliminates all units within the logarithm term, because each quantity
is divided by a standard concentration in the same units. Here are the
details for each type of reactant and product:
Solutes
For dilute (ideal) solutions, the standard state of the solute IS its molar
(not millimolar) concentration. So in this calculation, plug in
[NAD+] = 0.0200, and [NADH] = 0.0100.
Gases
The standard state for a gas is a pressure of 1 atm or 760 torr. So in
this calculation, plug in [O2] = 100 torr/760 torr = 0.132.
Hydrogen Ion
The biochemical standard state for hydrogen ion is pH 7, or 10-7
M. If the pH is 7.6, [H+] = 2.5 x 10-8. So in this
calculation, plug in [H+] = (2.5 x 10-8)/(10-7) =
0.251.
NOTE: The prime ['] on DG0' implies
that we are using biochemical standard states rather than conventional
thermodynamic standard states. In thermodynamics, the standard state for
the hydrogen ion is pH = 0 ([H+] = 1.00 M).
Water
The standard state for water is pure water, whose concentration is 55.5
M. In dilute aqueous solutions, the concentration of water is very close
to 55.5 M. So in this calculation, plug in [H2O] = 1.00. (NOTE:
In a cell, the total solute concentration is high, so the concentration
of water is certainly lower than 55.5 M. Nevertheless, biochemists commonly
use 1.00 as the activity of water.)
Calculation of the RT ln() Term:
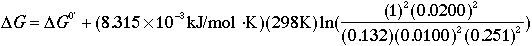
DG = DG0' + 15.3 kJ/mol.
(For an example of DG0' calculation,
see Summary of Energy Calculations.)
Summary
| Reaction Component |
How To Convert To Activity |
Example (Quantity => Activity) |
| Solute |
Convert concentration to molarity. Drop units. |
[solute] = 2.1 nM => 2.1 x 10-9 |
| Gas |
Divide partial pressure by 1 atm in same units. |
P(gas) = 45 kPa => 45/101.3 = .44 |
| H+ |
Divide molar concentration by 10-7 M (for biochemical standard state only). |
pH = 6 => 10-6 M/10-7 M = 10 |
| H2O |
For dilute solutions, use 1.00. (For concentrated solutions,
divide molarity of water by 55.5 M.) |
Dilute aqueous solution => 1.00 |
* Problems and Solutions to Accompany Rawn: Biochemistry, Neil Patterson Publishers, 1990, p. 157.
Back to Goodies List

![]()
![]()