Tips for Lab Reports
Table of Contents
Notebook
A major advice for successful experiments, besides learning the theoretical background, is keeping accurate report of your manipulations. Set up a lab notebook into which every experiment will be documented from the stage of planning, up to conclusions. The continuous development and improvement of it's shape and content will assist you far beyond the scope of the laboratory course.A good way to prepare yourself and your notebook for each day's lab
is to translate the procedure into a step-by-step check-list in the notebook,
leaving room between steps to enter observations and changes in procedure.
Make sure to define the composition of any common reaction mixture
(RM), out of available stock solutions of reagents, and a definition of
measured sample (volume, dilution, etc).
Also, set up tables for the data you will collect during the experiment,
including:
- a short , but descriptive title,
- the experimentally varied parameter (concentration, pH, tempetature, etc),
- the volume of added reagents (one column each, in the order of addition),
- raw data (e.g., absorbance, radioactivity, nb. of colonies, etc.),
- their units (in each column heading),
- final results (processed data).
Finally, include a sample calculation of the conversion factor (accounting
for time, concentration, etc.), used to process the raw data.
In all your decisions about what to put into your lab report, remember this guiding rule:
Your report should be a complete, stand-alone record of the experiment and its results. Anyone with at least your background in chemistry/biology should be able to go into the lab with nothing but your report to guide them, carry out the same experiment, and compare their data, calculations, graphs, and final results with yours.
BEFORE you prepare your lab report, your lab notebook should contain the following:
- Full, usable procedures that others could follow without referring to the lab manual.
- Records of observations made during the experiment.
- Data obtained, in tables.
- All calculations, showing proper use of units and significant digits.
- Final results, with the most important results displayed prominently.
- A brief summary (one or two paragraphs -- see sample below), describing your most important results and your assessment of their reliability, based on comparisons or successive runs and/or the precision of the lab equipment used.
Graphs
A graph should be able to stand alone as a description of an experimental system and its behavior (further insights).
Follow these guidelines for all graphs:
- Include the origin (0,0) at the lower left of the graph, if practical (not if logarithmic axes are used).
- Label the axes with variable names, followed by abbreviations of units of the variable in parentheses: Example: Concentration of S2O82- (eq/L).
- Divide the axes into easy-to-understand units. If needed, break the axes
into two separate ranges such that the first label in the second range is
positionned correctly, relative to both ranges, as in the following example:
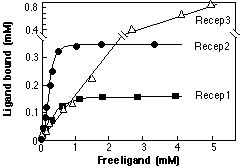
- Label clearly each plot in a multiple plots graph (see example above). If needed, use a descriptive table as an inset to the graph.
- Give an informative title that adds to, rather than repeats, the information on the axes. Example, for a graph of binding versus concentration: Dependence on ligand concentration of its binding to three receptors. The title should not simply reiterate the names of the variables; they are obvious to the reader if the axes are properly labeled.
- Provide any necessary additional information (remarks, differences from the standart protocol, etc.) in a legend to the graph.
- Display the equation of a line or curve fitted to the data (if applicable). Edit the equation to change the default variable names (x and y in usual graphing software) to the actual names of the variables you used in the plot.
Estimating Experimental Variation
(Sometimes Called Experimental Error)
This appendix can be used to assess the reliability or precision of any laboratory results.
Experimental variation is a measure of how reliable your lab results are, assuming that you carried out the procedure properly, and made all measurements with proper technique and care. It is sometimes called experimental error, but that term is misleading, because experimental variation tells you how precise your results are if you made no errors. Experimental variation depends only on the precision of your measuring tools. For more insight in experimental measurement and significant digits see active learning module at the Antoine project.
In the experiment on Kc for [FeSCN]2+, you used 5-mL graduated pipets to measure volumes, and you can read these pipets to a tolerance of about +/- 0.02 mL, in a 1-mL volume (assume this is the smallest volume you measured). This tolerance would introduce a maximum error of 0.02/1.00 = 2%. Because of drift in the last decimal place on the Spectrophotometer, you can read absorbance to a tolerance of about +/- .005 OD, in a reading of say 0.200 OD. This introduces a maximum error of 0.005/0.200, or 2.5%, in your smallest measured absorbance.
After you calculate Kc, if you calculate it again, but you increase [FeSCN2+] by 2.5% (because you determine it from A) and decrease [Fe3+] and [SCN-] by 2% (because these molarities depend mostly on volume measurements), this will compound the errors in the worst way possible, and give a value of Kc that contains the maximum expected error or variation. Try it for one of your calculated values of Kc. Here is an example:
Kc = [FeSCN2+] / [Fe3+] [SCN-]
A parenthesis here on the correct notations of chemical formulas of ions (e.g. Fe3+, SCN-, written without brackets), and ionic complexes (e.g. [FeSCN]2+, written in brackets with the final charge outside); however, their respective concentrations ([Fe3+], [SCN-], [FeSCN2+]), are all written in brackets with the charges inside.
Without error: Kc = (3.84 x 10-5 ) / (9.62 x 10-4 )(1.61 x 10-4 ) = 248.
Adding 2.5% to the numerator, and subtracting 2% from each molarity in the denominator gives this result:
With error: K'c = (3.94 x 10-5) / (9.43 x 10-4)(1.58 x 10-4) = 264.
The difference between Kc and K'c is 16, which is about 6.5% of 248. The maximum expected experimental variation in Kc is therefore 6.5%.
This example shows how to use the precision of lab instruments to estimate the expected variation in results. This method gives the maximum error you can expect in Kc if you make no blunders in lab.
| Rule: the maximal relative experimental variation on an expression is computed as the weighted sum of the relative variations of the experimental measurements. |
| For the expression:
where a-e are constant coefficients, A-E are measured variables, and m-q are exponents, the maximal relative experimental variation on Y is: where DA/A - DE/E are the relative errors on the experimental measurements of A-E (DA is the absolute error on the measurement of the measured value A). Note that the constant coefficients a-e do NOT contribute to the calculated variation. |
Finally, the final calculated values should be reported as Y +/- DY.
Sample Abstract
Summaries (or abstracts) should be writen informally in your notebook. You do not hand them in with your report, it helps you "extracting" the most relevant conclusions, trimming out the superfluous (often irrelevant and even erronneous) self-chat. Here is a sample summary:Empirical Formula of a Compoundby Vivian Johnson
I determined the empirical formula of bismuth oxide by finding the ratio [(moles O)/(moles Bi)] in a sample of the compound. I heated three weighed samples of finely divided bismuth in air and obtained a yellow oxide product. By comparing the measured weights of the oxide products with the original weights of the bismuth samples, I found the percent by weight of Bi and O. Then I calculated the molar ratio of O to Bi, obtaining a value of 2.46 +/- 0.17 for the three trials. This ratio corresponds to an empirical formula of Bi2O5, which is the formula of a known oxide of bismuth listed in the CRC Handbook of Chemistry and Physics.
Note that the abstract includes no specific details of procedure, and no specific intermediate quantities. The only quantities that Vivian provides are the results that constitute the goal of the experiment (the molar ratio of O to Bi), along with an estimate of its precision. The abstract ends with a brief interpretation of the meaning of the results, and a comparison with known values.