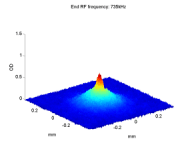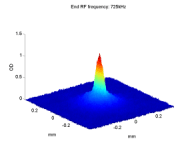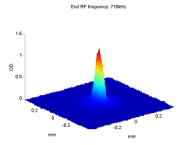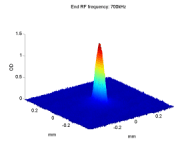
BEC2 Reaches the Phase Transition
The phase transition to Bose-Einstein condensation (BEC) occurs when the phase space density (the density of the atoms multiplied by their thermal wavelength cubed) becomes larger than one. The RF evaporation technique is able to bring the atomic cloud to the needed parameters. However, this technique requires a trap with a controllable depth, namely, that the height of the trap walls may be varied so hot atoms may be expelled. In our experiment, we use for this purpose a magnetic trap. These traps are typically not deep enough to trap atoms at room temperature and pre-cooling, to ~100µK, is necessary. In our system, we use a magneto-optical trap to cool and trap an atomic sample (from the background gas), as a preparatory step for the magnetic trap.
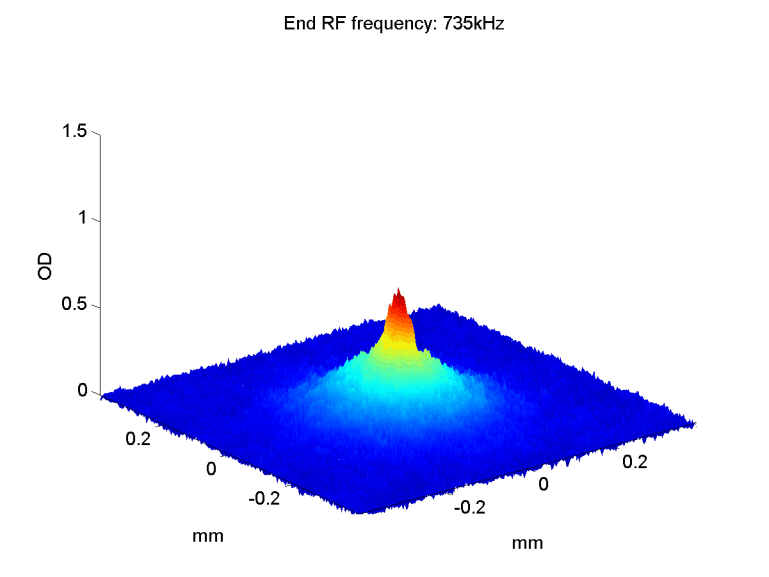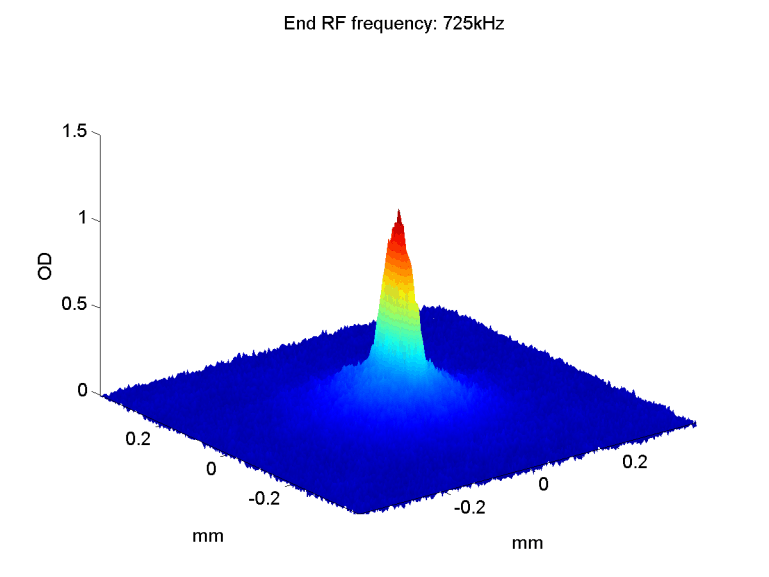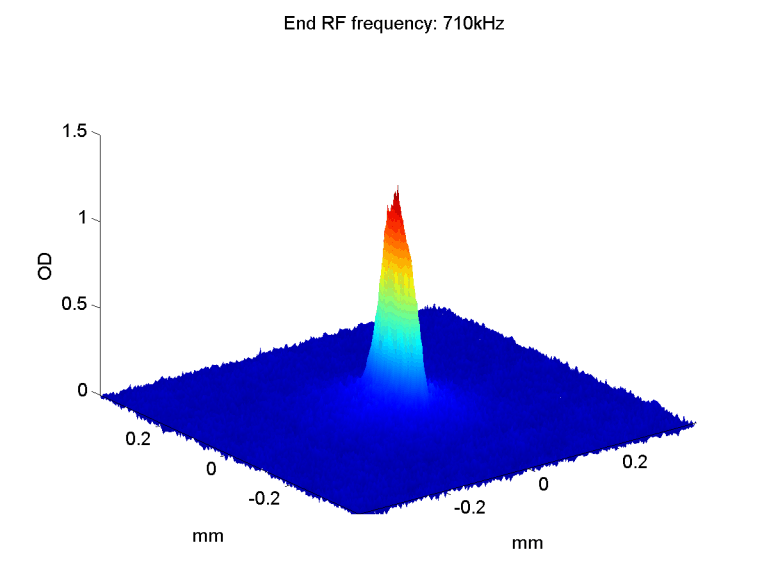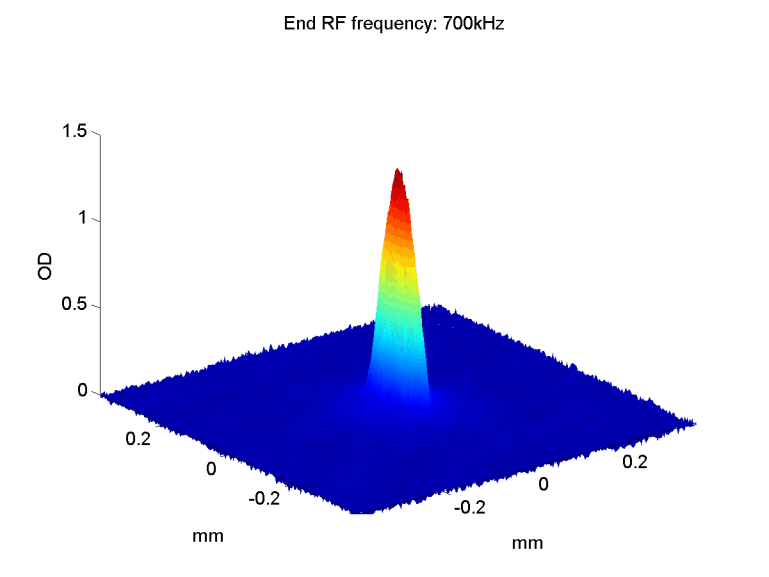
After cooling the atomic cloud through the phase transition, ~300nK, one should observe the differences between a Bose gas and a gas in a Maxwell-Boltzmann distribution. As long as the thermal gas does not reach the phase transition, or is very close to it, it is still considered an ideal gas that obeys the Maxwell-Boltzmann distribution. The velocity distribution has a Gaussian shape, and after release it expands isotropically.
Full size image |
When the atomic gas condenses, both the shape and the expansion after release change. In a non-interacting BEC, the shape of the condensed atoms is still a Gaussian, but much sharper than the thermal distribution. If the atoms are interacting, the condensate gets the trap shape - an inverted parabola. This parabola is much wider than the ground state Gaussian, but it is still much narrower than the broad thermal distribution. |
In addition, when releasing a BEC from the trap, its expansion depends significantly on the trap shape, setting the initial conditions. The cloud expands faster in the axis which was narrower in the trap, i.e. the tighter axis. When the atoms are non-interacting, this effect can be explained as a result of the uncertainty principle, ΔxΔp > ħ. In the tighter axis, Δx - the uncertainty in position, is smaller, and hence Δp - the uncertainty in momentum, is larger. If the atoms are interacting this anisotropic expansion is mostly due to the interaction energy converted into kinetic energy. |
 Full size image |