Dr. Aleksey
Drozdov
Theory of polymer chain conformation,
polymer network elasticity, scattering theory.
The activity of Dr. Alekey Drozdov is geared towards
providing the theoretical framework for the study of polymers in the
melt state, in crosslinked networks, in filled systems and on surfaces.
Its main goal is to derive from chain conformation and statistical thermodynamics
principles experimentally accessible variables such as stress-strain
behavior and scattering intensity. Many of the problems solved theoretically
are closely related to issues dealt with experimentally by other RSMC
members.
1. Single chain conformation
The end-to-end distribution function for a flexible chain with weak
excluded-volume interactions. An explicit expression is derived for
the distribution function of end-to-end vectors and for the mean square
end-to-end distance of a flexible chain with excluded-volume interactions.
The Hamiltonian for a flexible chain with weak intra-chain interactions
is determined by two small parameters: the ratio e of the energy of
interaction between segments (within a sphere whose radius coincides
with the cut-off length for the potential) to the thermal energy, and
the ratio d of the cut-off length to the radius of gyration for a Gaussian
chain. Unlike conventional approaches grounded on the mean-field evaluation
of the end-to-end distance, the Green function is found explicitly (in
the first approximation with respect to e). It is demonstrated that
(i) the distribution function depends on e in a regular way, while its
dependence on d is singular, and (ii) the leading term in the expression
for the mean square end-to-end distance linearly grows with e and remains
independent of d.
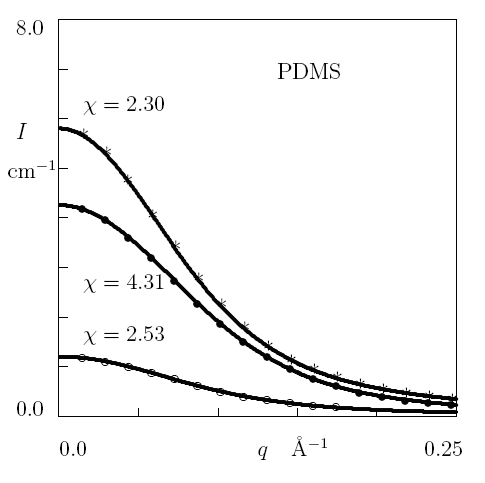
Fig. 1A: The scattering intensity I
versus the amplitude of scattering vector q. Symbols: experimental data
on H-PDMS/D-PDMS blends at volume fractions of H-PDMS 0.06 (unfilled
circles), 0.26 (filled circles), and 0.52 (asterisks). Solid lines:
results of numerical simulation.
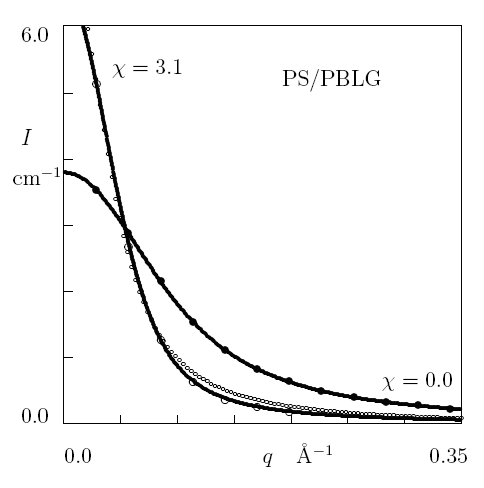
Fig. 1B: The scattering intensity I
versus the amplitude of scattering vector q. Large symbols: experimental
data on solutions of PS/PBLG in dioxane (unfilled circles) and dioxane/TFA
mixture (filled circles). Solid lines: results of numerical simulation.
Small circles: approximation by the Debay function with b = 137:2 nm.
Scattering function for a self-avoiding polymer chain.
An explicit expression is derived for the scattering function of a self-avoiding
polymer chain in a d-dimensional space. The effect of strength of segment
interactions on the shape of the scattering function and the radius
of gyration of a chain is studied numerically. Excellent agreement is
demonstrated between experimental data on dilute solutions of several
polymers and results of numerical simulation as depicted in Fig. 1.
Stiffness of polymer chains. A formula is derived for
stiffness of a polymer chain in terms of the distribution function of
end-to-end vectors. This relationship is applied to calculate the stiffness
of Gaussian chains (neutral and carrying electric charges at the ends),
chains modeled as self-avoiding random walks, as well as semi-flexible
(worm-like and Dirac) chains. The effects of persistence length and
Bjerrum's length on the chain stiffness are analyzed numerically. An
explicit expression is developed for the radial distribution function
of a chain with the maximum stiffness.
2. Constitutive Equations for Polymer Networks
A constitutive model for non-affine polymer networks that accounts for
stretching of chains. Derivation of constitutive equations for branched
polymer melts within the concept of polymer networks with sliding junctions
and numerical analysis of the effect of sliding on the mechanical response.
A model is derived for isothermal deformation of polymer fluids. A polymer
is treated as a permanent network of chains bridged by junctions (entanglements).
Macro-deformation of a fluid induces two motions at the micro-level:
sliding of junctions with respect to their reference positions in the
bulk medium and slippage of chains with respect to entanglements that
is associated with unfolding of back-loops.
Constitutive equations are developed by using the laws of thermodynamics.
Three important features distinguish the present model from other constitutive
relations that account for stretching of chains: (i) the symmetry of
interactions between the elongation of strands and an analog of the
configurational tensor (in the sense that the former variable is included
into the kinetic equation for the latter and vise versa), (ii) the strong
nonlinearity of the governing equations, and (iii) the account for an
elastic interaction between chains driven by volumetric deformation
that reflects to their stretching.
The governing equations are applied to the numerical analysis of uniaxial
extensional and shear flows. It is demonstrated that the model describes
qualitatively characteristic features of the time-dependent response
of polymer melts and solutions observed in conventional rheological
tests.
Non-entropic theory of rubber elasticity: flexible
chains with weak excluded-volume interactions. Strain energy density
is calculated for a network of flexible chains with weak excluded-volume
interactions (whose energy is small compared with thermal energy). Constitutive
equations are developed for an incompressible network of chains with
segment interactions at finite deformations. These relations are applied
to the study of uniaxial and equi-biaxial tension (compression), where
the stress–strain diagrams are analyzed numerically. It is demonstrated
that intra-chain interactions (i) cause an increase in the Young’s modulus
of the network and (ii) induce the growth of stresses (compared to an
appropriate network of Gaussian chains), which becomes substantial at
relatively large elongation ratios. The effect of excluded-volume interactions
on the elastic response strongly depends on the deformation mode, in
particular, it is more pronounced at equi-biaxial tension than at uniaxial
elongation.
Networks of self-avoiding chains and Ogden-type constitutive equations
for elastomers. An expression is derived for the strain energy of a
polymer chain under an arbitrary three dimensional deformation with
finite strains. For a Gaussian chain, this expression is reduced to
the conventional Moony–Rivlin constitutive law, while for non-Gaussian
chains it implies novel constitutive relations. Based on the three-chain
approximation, explicit formulas are developed for the strain energy
of a chain modeled as a self-avoiding random walk. In the case of self-avoiding
chains with stretched-exponential distribution function of end-to-end
vectors, the strain energy density of a network is described by the
Ogden law with only two material constants. For the des Cloizeaux distribution
function, the constitutive equation involves three adjustable parameters.
The governing equations are verified by fitting observations on uniaxial
tension, uniaxial compression and biaxial tension of elastomers. Good
agreement is demonstrated in Fig. 2 between the experimental data and
the results of numerical analysis. An analytical formula is derived
for the ratio of the Young’s modulus of a self-avoiding chain to that
of a Gaussian chain. It is found that the elastic modulus per chain
in the Ogden network exceeds that in a Gaussian network by a factor
of three, whereas the elastic modulus of a chain with the generalized
stretched exponential distribution function equals about half of the
modulus of a Gaussian chain.
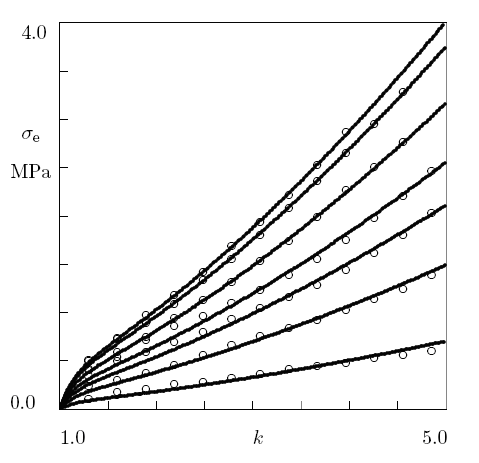
Fig 2A: The engineering stress se versus elongation ratio
k at uniaxial extension of natural rubber with the concentration of
cross-linker f = 1.0, 1.5, 2.0, 2.5, 3.0, 3.5 and 4.0 phr, from bottom
to top, respectively. Circles: experimental data. Solid lines: results
of numerical simulation.
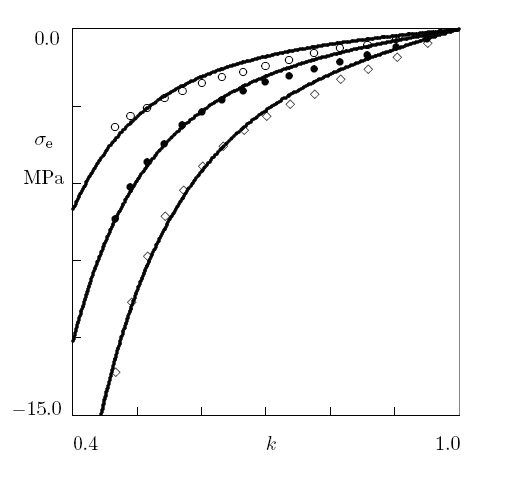
Fig. 2B: The engineering stress se versus
elongation ratio k at uniaxial compression of chloroprene rubber reinforced
with carbon black (CB). Symbols: experimental data. Unfilled circles:
15 phr CB. Filled circles: 40 phr CB. Diamonds: 65 phr CB. Solid lines:
results of numerical simulation.
On going work also includes development of theory to support experimental
work related to polymer- surface and polymer-interface interactions
carried out in Prof. Gottlieb's group: (i) Theoretical and numerical
analysis of the mechanical response of flexible polymer chains tethered
at a rigid surface and polymer brushes. (ii)Study of the lateral mobility
and spatial organization of a monolayer of flexible chains tethered
at the air–aqueous solution interface with account for excluded-volume
interactions between macromolecules.

